布尔逻辑的应用

文章摘要：有多种不同的方法来实现该表，在此我们将介绍一种易于理解的方法。如果您查看Q位，会发现顶部4位的工作方式与针对A 和B的异或门电路类似，而底部4位的工作方式与针对A和B的同或门电路类似。同样，CO顶部4位的工作方式与针对A和B的与门电路类似，而底部4位的工作方式则和或门电路类似。根据这些事实，下面的电路可实现全加法器： 这当然不是实现全加法器最有效的方法，但却极易理解，并且很容易跟踪使用该方法的逻辑。如果有兴趣，您可以思考一下如何使用更少的门电路来实现该逻辑。 现在我们有了一个名为“全加法器”的功能。计算机工程师下一步要做的是将全加法器装在“黑盒子”中，这样他就不用考虑该元件的细节了。用于全加

布尔逻辑的应用,标签：电子电路基础,模拟电路基础,http://www.88dzw.com

有多种不同的方法来实现该表，在此我们将介绍一种易于理解的方法。如果您查看Q位，会发现顶部4位的工作方式与针对A 和B的异或门电路类似，而底部4位的工作方式与针对A和B的同或门电路类似。同样，CO顶部4位的工作方式与针对A和B的与门电路类似，而底部4位的工作方式则和或门电路类似。根据这些事实，下面的电路可实现全加法器：

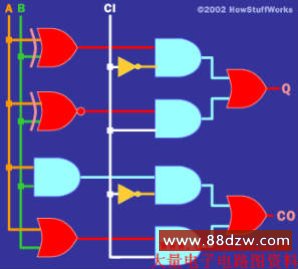
这当然不是实现全加法器最有效的方法，但却极易理解，并且很容易跟踪使用该方法的逻辑。如果有兴趣，您可以思考一下如何使用更少的门电路来实现该逻辑。

现在我们有了一个名为“全加法器”的功能。计算机工程师下一步要做的是将全加法器装在“黑盒子”中，这样他就不用考虑该元件的细节了。用于全加法器的黑盒子将如下所示：

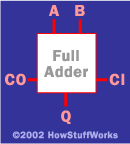
通过这个黑盒子，现在很容易就可画出一个4位全加法器：

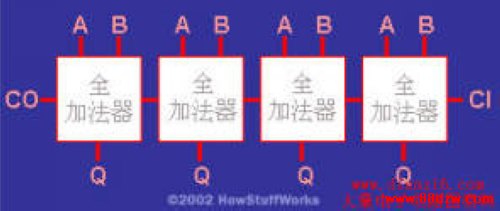
在该电路图中，每一位的进位输出将直接输入到下一位的进位输入。通过硬连线方式将最初的进位输入位设为0。如果在A和B线路上输入两个4位的数字，则将会在Q线路上获得该4位数的和输出，另外还有1位用来表示最终进位输出。你会发现该链可随意扩展，如果需要，可扩展到8位、16位或32位。

我们刚刚创建的4位加法器称为行波进位加法器。之所以称为行波进位加法器，是因为进位位像波纹一样从一个加法器输入到另一加法器。该实现方式的优点在于它非常简单，但其缺点是存在速度问题。在实际电路中，门电路的状态切换需要时间（该转换时间属于纳秒级，但对于高速计算机来说纳秒也是很重要的）。由于存在行波进位，因此32或64位的行波进位加法器可能需要100到200纳秒来获得最终的求和结果。为此，工程师创建了更高级的名为先行进位加法器的加法器。实现先行进位加法器所需的门电路数量很大，但是该加法器在计算速度上大有改进。

触发器

通过布尔门电路可以实现的一项更为有趣的功能是形成记忆。如果门电路的连接正确，它们将会记住输入值。这一简单概念成为计算机中RAM（随机存取存储器）的基础，并且还使得创建其他各种有用的电路成为可能。

记忆依赖于一个名为反馈的概念，也就是说门电路的输出将反馈给输入。下面显示的是使用两个反相器的最简单的反馈电路：

如果沿着反馈路线，则会看到如果Q为1，则它始终为1；如果Q为0，则它始终 0。由于有必要控制所创建的电路，因此上面的电路没有多大用处，但它能够使您了解反馈的工作方式。

事实上，在“真正”的电路中，可使用这类简单的反相器反馈方法。下面显示了一种更有用的使用两个与非门电路的反馈电路：

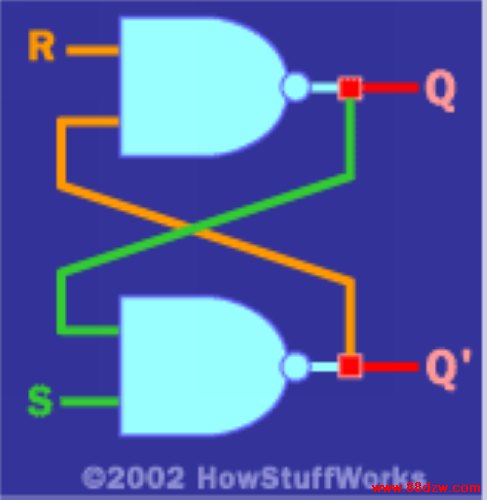
该电路有两个输入（R和S）和两个输出（Q和Q'）。由于存在反馈，因此该电路的逻辑表与先前看到的逻辑表相比有些不同。

上一页  [1] [2] [3] [4] [5] [6] [7]  下一页