基于FPGA的高速流水线浮点乘法器设计

文章摘要：摘要：设计了一种支持IEEE754浮点标准的32位高速流水线结构浮点乘法器。该乘法器采用新型的基4布思算法,改进的4:2压缩结构和部分积求和电路,完成Carry Save形式的部分积压缩,再由Carry Look-ahead加法器求得乘积。时序仿真结果表明该乘法器可稳定运行在80M的频率上,并已成功运用在浮点FFT处理器中。1 引言在数字化飞速发展的今天，人们对微处理器的性能要求也越来越高。作为衡量微处理器 性能的主要标准，主频和乘法器运行一次乘法的周期息息相关。因此，为了进一步提高微处 理器性能，开发高速高精度的乘法器势在必行。同时由于基于IEEE754 标准的浮点运算具 有动态范围大，可实

基于FPGA的高速流水线浮点乘法器设计,标签：eda技术,eda技术实用教程,http://www.88dzw.com

　　摘要：设计了一种支持IEEE754浮点标准的32位高速流水线结构浮点乘法器。该乘法器采用新型的基4布思算法,改进的4:2压缩结构和部分积求和电路,完成Carry Save形式的部分积压缩,再由Carry Look-ahead加法器求得乘积。时序仿真结果表明该乘法器可稳定运行在80M的频率上,并已成功运用在浮点FFT处理器中。

　　1 引言

　　在数字化飞速发展的今天，人们对微处理器的性能要求也越来越高。作为衡量微处理器 性能的主要标准，主频和乘法器运行一次乘法的周期息息相关。因此，为了进一步提高微处 理器性能，开发高速高精度的乘法器势在必行。同时由于基于IEEE754 标准的浮点运算具 有动态范围大，可实现高精度，运算规律较定点运算更为简捷等特点，浮点运算单元的设计 研究已获得广泛的重视。 本文介绍了 32 位浮点乘法器的设计，采用了基4 布思算法，改进的4：2 压缩器及布思 编码算法，并结合FPGA 自身特点，使用流水线设计技术，在实现高速浮点乘法的同时，也 使是系统具有了高稳定性、规则的结构、易于FPGA 实现及ASIC 的HardCopy 等特点。

　　2 运算规则及系统结构

　　2.1 浮点数的表示规则

　　本设计采用单精度IEEE754 格式【2】。设参与运算的两个数A、B 均为单精度浮点数， 即：

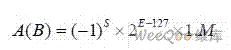
　　2.2 浮点乘法器的硬件系统结构

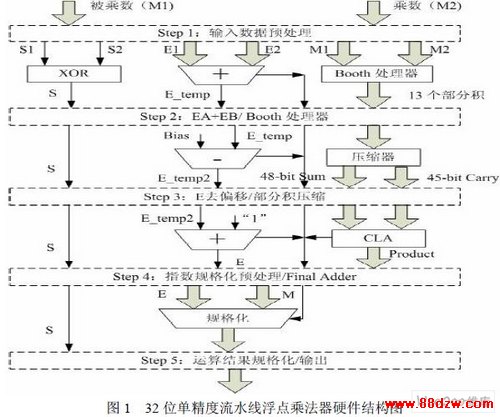
　　本设计用于专用浮点FFT 处理器，因此对运算速度有较高要求。为了保证浮点乘法器 可以稳定运行在80M 以下，本设计采用了流水线技术。流水线技术可提高同步电路的运行 速度，加大数据吞吐量。而FPGA 的内部结构特点很适合在其中采用流水线设计，并且只需 要极少或者根本不需要额外的成本。综上所述，根据系统分割，本设计将采用5 级流水处理， 图1 为浮点乘法器的硬件结构图。

　　3 主要模块设计与仿真

　　3.1 指数处理模块（E_Adder）设计

　　32位浮点数格式如文献【2】中定义。由前述可知，浮点乘法的主要过程是两个尾数相 乘，同时并行处理指数相加及溢出检测。对于32位的浮点乘法器而言，其指数为8位，因而 本设计采用带进位输出的8位超前进位加法器完成指数相加、去偏移等操作，具体过程如下。

　　E_Adder 模块负责完成浮点乘法器运算中指数域的求和运算，如下式所示：

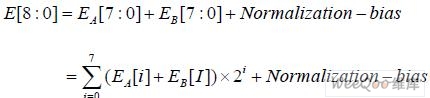
　　其中，E[8]为MSB 位产生的进位。Bias=127 是IEEE754 标准中定义的指数偏移值。 Normalization 完成规格化操作，因为指数求和结果与尾数相乘结果有关。在本次设计中，通 过选择的方法，几乎可以在Normalization 标志产生后立刻获得积的指数部分，使E_Adder 不处于关键路径。

　　本设计收集三级进位信号，配合尾数相乘单元的 Normalization 信号，对计算结果进行 规格化处理，并决定是否输出无穷大、无穷小或正常值。

　　根据 E_Adder 的时序仿真视图，可看出设计完全符合应用需求。

　　3.2 改进的Booth 编码器设计

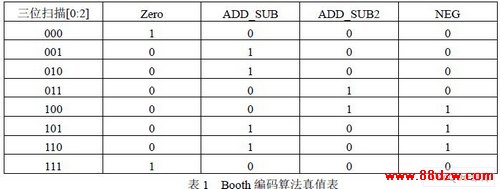
　　由于整个乘法器的延迟主要决定于相加的部分积个数，因此必须减少部分积的数目才能 进而缩短整个乘法器的运算延迟。本设计采用基4 布思编码器，使得部分积减少到13 个， 并对传统的编码方案进行改进。编码算法如表1 所示。

[1] [2]  下一页