定点小数的编码方法

文章摘要：0应为0，[X]补= 2*0 + X = X，X为负时，X0应为1，[X]补 = 2*1+X = 2 + X ，均与补码的定义吻合。由此又可以得到从[X]补求X的关系，即由机器数求其代表的真值的关系如下:X = [X]补 - 2X0= X0X1X2…Xn - 2X0= -X0 + 0.X1X2…Xn (2.12)当X为正数时，X0=0 真值 X = [X]补 ; 当X为负数时，X0=1 真值 X = -1 + 0.X1X2…Xn = -(1-0.X1X2…Xn)。对补码的数值部分求补，并加上符号即得真值。例如［Ｘ补＝10110，则Ｘ的真值 = -(1-0.0110) = -0.1010。当已知

定点小数的编码方法,标签：电子电路基础,模拟电路基础,http://www.88dzw.com
0应为0，[X]_补= 2*0 + X = X，X为负时，X₀应为1，[X]_补 = 2*1+X = 2 + X ，均与补码的定义吻合。由此又可以得到从[X]补求X的关系，即由机器数求其代表的真值的关系如下:
　　　X = [X]_补 - 2X₀
　　　　= X₀X₁X₂…X_n - 2X₀
　　　　= -X₀ + 0.X₁X₂…X_n (2.12)

　　当X为正数时，X₀=0 真值 X = [X]_补 ;
　　当X为负数时，X₀=1 真值 X = -1 + 0.X₁X₂…X_n = -(1-0.X₁X₂…X_n)。
　　对补码的数值部分求补，并加上符号即得真值。

　　例如［Ｘ_补＝10110，则Ｘ的真值 = -(1-0.0110) = -0.1010。当已知补码而需求此数的真值时可采用此法，此公式在推导补码乘法的运算算法中很有用。

　　⑤ 补码的算术移位
　　将[X] _补的符号位与数值位一起右移一次并保持原符号位的值不变，可实现除法功能(除以2)，即[X/2]_补= X₀X₀X₁X₂…X_n-1X_n。今考虑X为正、负数两种情况。
　　
　　设: X= 0.0110, [X]_补=00110,右移一位得00011，是X除以2的补码结果。
　　设: X=-0.0110，[X]_补=11010，计算 [X/2]_补=11101，再按④求真值得X/2=-0.0011，说明得到的确实是X除以2的结果。

　　为了得到一个数的补码表示，当然可以通过补码的定义求得,但更简便的办法是：
　　当X≥0时，[X]_补的符号位取0，数值位取X的各数值位上的值，此时有[X] _补=[X] _原。

　　当X<0时，[X]_补的符号位取1，将X的各数值位取反(0变1,1变0)再在最低位加1，以得到 [X]补的各数值位上的值。

　　从[X]_原求 [X] _补时,对正数或零,有[X] _补=[X]_原，对负数，是符号位不变，各数值位变反后再在最低位执行加1操作。同理,由[X]_补求 [X]_原时，对负数仍是符号位不变，各数值位变反后再在最低位执行加1操作。

　　在说明补码的性质(3)时，特别强调两个数的补码相加，仅在其运算结果不超出机器能表示的数值范围时，运算结果才是正确的，否则得到的结果不正确。如[X]补+[Y]补=01001+01010=10011。两个大于0.5的正数相加，结果的符号位变成负号，数值部分也是错误的。这是因此参加运算的两个数的和大于1，超出了机器所能表示的范围，产生了所谓的 "溢出"。对负数也会产生溢出，如[X]_补+[Y]_补=10101+10100=01001，两个负数相加，结果的符号位却变成正号，说明结果是错误的。

　　为了方便判别结果是否溢出,某些机器采用变形补码,又称模4补码表示方法,其定义为：

　　　　[X]_补=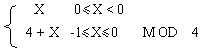 (2.13)

　　也就是常说的双符号位的补码表示。例如:
　　　　X=+0.1011， [X]_补=001011
　　　　X=-0.1011， [X]_补=110101
　　
　　按模4补码定义，当X=-0.1011时，[X]_补= 4+X = 100.0000+(-0.1011) = 110101。从上式的结果可以看出，模4补码的表示就是在模2补码表示的符号位之前再增加与原符号同值的另一个符号位。

　　模4补码的性质:
　　① 模4补码的两个符号位相同，00表示正号，11表示负号，其数值位与其模2补码相同。当符号位为01或10时，表示数值溢出。01表示两个正数相加之和≥1的情况，通称数值 "上溢"；为10时,表示两个负数相加，而其和小于-1的情况，通称数值 "下溢"。前面的1个符号位是正确的符号位。

　　② 在模4补码表示中,零有唯一的编码,即 [+0.0]_补 = [-0.0]_补= 000000。模4补码能表示-1，即为110000，与模2补码的情况非常类似。

上一页  [1] [2] [3]  下一页