非正弦周期信号的傅里叶级数分解

文章摘要：称为基波角频率；二式中系数之间有关系式：或 （6-1-3）展开式中除第一项外,每一项都是不同频率的正弦量，称为周期函数的直流分量（恒定分量），第二项称为基波分量，基波角频率，其变化周期与原函数周期相同，其余各项（的项）统称为高次谐波。高次谐波分量的频率是基波频率的整数倍。当时称为二次谐波，时称为三次谐波等等。是第n次谐波的初相角。当已知时，傅里叶级数表达式中各谐波分量的系数可由下面公式求得： （6-1-4）下面用一个具体例子来进行傅里叶分解。例6-1-1 图6-1-1所示为对称方波电压，其表达式可写为：上一页 [1] [

非正弦周期信号的傅里叶级数分解,标签：电子电路基础,模拟电路基础,http://www.88dzw.com
称为基波角频率；二式中系数之间有关系式：

或 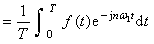                          （6-1-3）

展开式中除第一项外,每一项都是不同频率的正弦量，称为周期函数的直流分量（恒定分量），第二项称为基波分量，基波角频率，其变化周期与原函数周期相同，其余各项（的项）统称为高次谐波。高次谐波分量的频率是基波频率的整数倍。当时称为二次谐波，时称为三次谐波等等。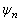是第n次谐波的初相角。

当已知时，傅里叶级数表达式中各谐波分量的系数可由下面公式求得：

         （6-1-4）

下面用一个具体例子来进行傅里叶分解。

例6-1-1   图6-1-1所示为对称方波电压，其表达式可写为：

上一页  [1] [2] [3] [4] [5] [6] [7] [8] [9]  下一页